Section 11: Numerical Integration
About the Algorithm
The Math Pac uses a Romberg method for accumulating the value of an integral. Several refinements make it more effective. Instead of equally spaced samples, which can introduce a kind of resonance or aliasing that produces misleading results when the integrand is periodic, INTEGRAL uses samples that are spaced nonuniformly. Their spacing can be demonstrated by substituting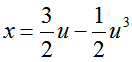 into
into 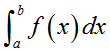
and then spacing u uniformly. Besides suppressing resonance, the substitution has two additional benefits. First, no sample need be taken from either endpoint of the interval of integration unless the interval is so small that points in the interval round to an endpoint. As a result, an integral like
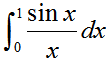
will not be interrupted by division by zero at an endpoint. Second, INTEGRAL can
integrate functions whose slope is infinite at an endpoint. Such functions
are encountered when calculating the area enclosed by a smooth closed curve
like ![]() .
.
In addition, INTEGRAL uses extended precision. Internally, sums are accumulated in 15-digit numbers. This allows thousands of samples to be accumulated, if necessary, without losing any more significance to round-off than is lost within your function.
During the computation, INTEGRAL generates a sequence of iterates that are increasingly accurate estimates of the actual value of the integral. It also estimates the width of the error ribbon at each iterate. INTEGRAL stops only after three successive iterates are within the computed error of each other or after 16 iterations have been performed without this criterion being met.
In the latter case the function will have been sampled at 65,535 points. The value returned by IBOUND will be the negative of the computed error to signify that the returned value of the INTEGRAL is likely not within the error tolerance of the actual value. Typically, you should then split up the interval of integration into smaller subintervals and integrate the function over each of the subintervals. The integral over the original interval will then be the sum of the integrals over the subintervals. In this way, up to 65,535 points can be sampled on each subinterval, thus computing the integral to greater precision.
In summary, INTEGRAL has been designed to return reliable results rapidly and in a convenient, easy-to-use fashion. The above theoretical considerations discuss problems with numerical integration in general. The INTEGRAL keyword is capable of handling even difficult integrals with relative ease.